50. 단순회귀분석
1) 단순회귀분석의 모형
(1) 단순회귀분석(simple regression analysis): 하나의 독립변수와 종속변수와의 관
계를 선형관계식으로 표시하고, 독립변수와 종속변수에 대한 관찰자료를 이용하여
회귀계수(α와 β)를 추정하는 통계기법

■ α: 회귀식의 절편(intercept)으로 독립변수 X의 관찰값이 0일 때, 종속변수 Y의 값을 나타내
는 수치
■ β: 기울기로 독립변수 X의 한 단위 변화가 종속변수 Y의 값에 미치는 효과를 나타내는 계수
(2) 회귀분석은 독립변수와 종속변수 간의 관계를 보여주는 산포도 상에서 이들 두
변수들간의 관계를 가장 잘 나타내는 회귀선(regression line)을 찾아내는 방법으
로도 기술할 수 있음
(3) 회귀선으로 설명되지 못하는 부분이 오류항 ε임

2) 선형적 관계 중요성
(1) 사회과학 영역에서는 모든 데이터 측정 시, 오차가 발생하게 됨
(2) 관계식을 선형으로 표현하게 되면, 나타날 수 있는 오류가 평균적으로 서로 상쇄
되어 비선형인 접근법보다 나쁘지 않은 결론을 도출할 수 있음
(3) 선형 관계식은 쉽게 해법을 찾거나 풀 수 있으나 비선형이 되면 처리하는 속도가
상대적으로 느려짐
(4) 선형관계를 가정하면 각 변수들이 유사한 성질을 가지게 되므로, 상관관계 파악이
보다 용이해짐

3) 단순회귀분석의 가정
(1) 최소자승법을 이용한 단순회귀모형에서 오류항 ε에 대한 가정
| ■ 오류항 εi의 기댓값은 0이다. ■ 오류항 εi의 분산은 모든 관측치에 대하여 동일한 분산을 갖는다. ■ 오류항 εi는 정규분포를 따르며, 각 관측치들의 분산은 서로 독립적이다. |

4) 최소자승법을 이용한 모수(회귀계수) 추정방법
(1) 오류항에 대한 가정이 충족되면, 독립변수와 종속변수 간 관계를 파악하기 위한
두 모수(회귀계수) α, β를 추정해야 함
(2) 최소자승법: 잔차*(residual) 제곱의 합을 최소화시키도록 α, β의 추정값(또는 회
귀식)을 구하는 것
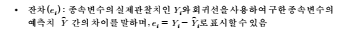

5) 단순회귀분석모형 산출 예시
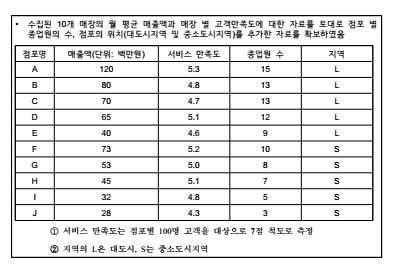
(1) 사례 설정
| ■ 신사복 제조업체는 치열한 경쟁 속에서 제품 차별화를 위한 많은 노력을 기울여 왔음. 점차 브랜드 간 제품 속성의 차이가 줄어듬에 따라 점포 내의 서비스와 같은 제품 외의 속성이 중요해지고 있음 ■ 이에 따라 L社의 남성 정장 브랜드 M은 10개의 매장을 선정하여 점포 서비스에 대한 소비자 만족도를 조사하고, 이를 매장별 매출액과 비교하여 두 변수간에 어떤 관계가 있는 지를 파악하고자 함 |
(2) 분석 환경 설정
(3) 회귀계수 산출 과정
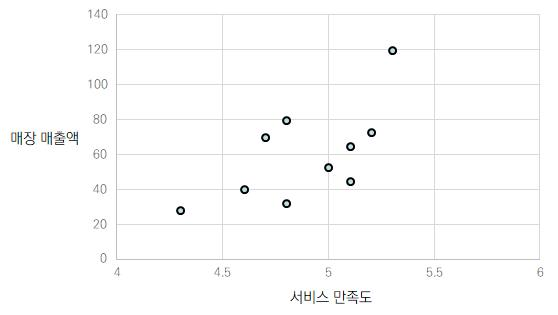
■ 먼저 매장별 매출액과 서비스 만족도 간의 관찰값에 대한 산포도를 이용하여, 두 변수 간 상
관관계를 시각적으로 살펴보기로 함
- 다음과 같이 두 변수 간에는 양의 상관관계가 있음을 알 수 있음
- 즉 고객서비스 만족도가 높아짐에 따라 점포의 매출 수준이 향상되고 있다고 판단할 수
있음
■ 최소자승법을 통해 두 변수 간의 관계를 정확히 반영할 수 있는 추정계수를 구함

- 이를 위해 다음의 표와 같이 회귀계수 추정을 위한 도표를 작성함
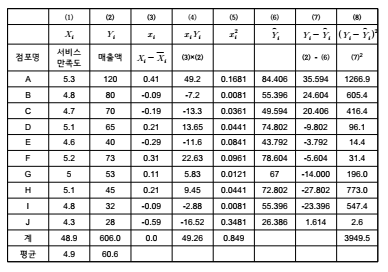
(4) 결과해석
■ 두 변수 간의 관계를 설명해 주는 회귀식은 다음과 같이 도출됨

■ 회귀식은 또 다른 용도로 활용 가능함

6) 추정된 회귀계수(독립변수)의 유의성과 설명력에 대한 평가
(1) 추정회귀계수(독립변수)에 대한 유의성 검증
■ 회귀변수에 대한 추정이 이루어지면, 산출된 값이 통계적으로 의미가 있는 지의 여부를 검증
하여야 함
- 이를 위해 다음과 같이 가설이 설정됨

■ 가설검증에 사용되는 통계량은 t통계량이며, n-2(n = 표본 수)의 자유도를 가지는 t분포를
따르게 됨

7) 회귀모형의 적합도(독립변수의 설명력)
(1) 추정된 회귀계수에 대한 유의성 검증과 함께 조사자는 추정된 회귀식이 독립변수
와 종속변수 간의 관계를 얼마나 잘 설명하는 지를 검토해야 함
■ 모델 적합도(model fitness): 추정된 회귀식이 종속변수의 변화(분산)에 대해 어느 정도의
설명력을 가지는 지를 검토하는 것
■ 결정계수(Coefficient of determination, R2): 0에서 1사이의 값을 가지며, 1에 가까울수록
회귀식의 설명력(적합도)이 커짐
(2) 결정계수는 Y(종속변수)의 평균으로부터의 총변동 중 회귀식에 의해 설명되는 부
분이 차지하는 비율(B/A)로 정의될 수 있음
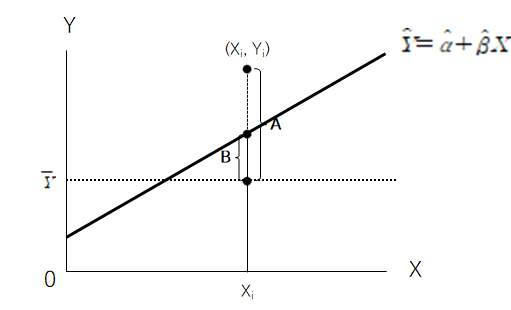
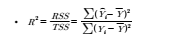
- RSS(Regression Sum of Squares: 회귀제곱합, 그림에서 B 부분)
- TSS(Total Sum of Squares: 총제곱합, 그림에서 A 부분)
■ 본 사례에서 결정계수(R2)는 0.42가 나왔는데, 이는 Y전체 변동(또는 분산) 중 42%가 회귀
식에 의해 설명됨을 의미함
- 단순회귀분석에서의 결정계수는 상관계수의 제곱과 일치함
(3) [참조] 모형 적합도의 의미
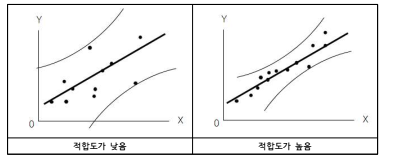
8) 회귀분석모형에 대한 유의성 검증
(1) 회귀분석에서는 추정된 회귀식의 설명력을 검토하기 위해 결정계수와 함께 회귀
식 전체의 유의성에 대한 F검증을 추가적으로 실시함
(2) F검증은 종속변수의 총분산이 독립변수 전체(또는 회귀식)에 의해 충분히 설명될
수 있는지를 검증하는 것으로 F통계량이 사용됨
(3) 이를 위해 다음과 같이 가설이 설정됨

(4) 가설검증에 사용되는 F통계량은 다음의 식으로 표시됨

9) SPSS를 이용한 단순회귀프로그램 운용
(1) [분석] - [회귀분석] - [선형]을 선택한 후, 분석하고자 할 독립변수와 종속변수
를 각각 입력하면 됨
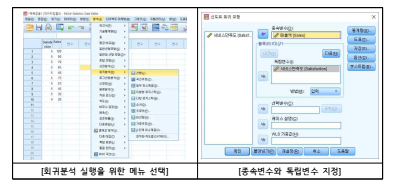
(2) 결과 해석
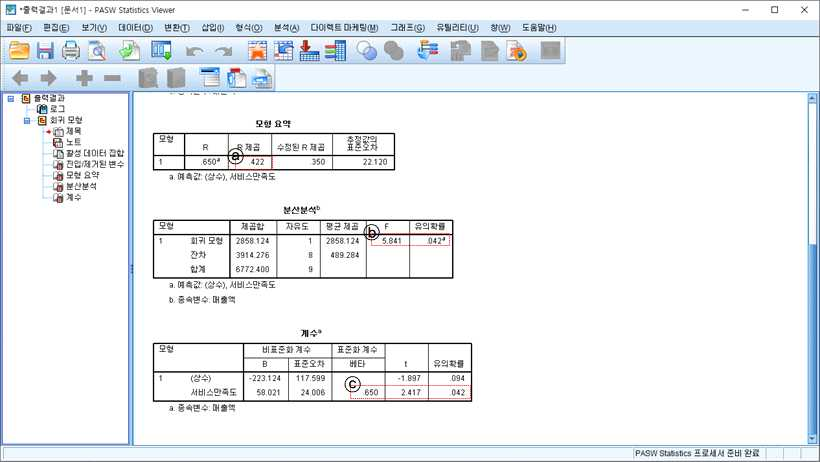
■ 회귀식: Y(매출액) = -223.12 + 28.02X1(서비스만족도)
■ ⓐ: 추정된 회귀식이 Y의 전체분산 중 42%를 설명하고 있음
■ ⓑ: 전체모형의 유의성에 대한 F검증 결과 유의수준 0.05에서 유의한 것으로 나타남. 즉
추정된 회귀모형이 관찰값을 잘 설명하고 있음
■ ⓒ: 독립변수(서비스만족도)에 대한 통계적 유의성에서 유의수준 0.05에서 유의한 것으로
나타남. 즉 추정된 회귀계수가 0이라는 귀무가설이 기각됨
'시장조사론' 카테고리의 다른 글
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 52. 판별 분석 개념 (2) | 2024.07.05 |
|---|---|
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 51. 다중회귀분석 (1) | 2024.07.04 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 49. 회귀 분석 개념 (1) | 2024.07.02 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 48. 상관계수 유의성 검증 (2) | 2024.07.01 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 47. 상관계수의 의미 (0) | 2024.06.30 |



