45. 분산분석
1) 이용상황
(1) 분산분석(ANOVA: Analysis of Variance): 명목척도로 측정된 독립변수와 등간
또는 비율척도로 측정된 종속변수 사이의 관계를 분석하는 기법
♤ 즉 독립변수에 의해 분류된 2개 이상의 집단 간의 평균값(종속변수 혹은 결과변수의 값)을
비교하는 데 사용되는 통계기법
♤ 검증통계량은 F-값을 사용함

(2) 분산분석 적용 사례
♤ 10대와 20대 세분 시장간에 선호하는 청바지의 가격 차이 여부
♤ 서울 강남의 압구정동과 강북지역 주부들 간 한 달간 백화점 쇼핑횟수 차이 여부
♤ 대리점, 직영점 등 서로 다른 유통형태에 따라 매출이나 이익의 차이 여부 등
(3) 분산분석의 유형
♤ 일원분산분석(One-way ANOVA): 하나의 범주형 독립변수와 종속변수 간의 관계
♤ 다원분산분석(n-way ANOVA): 2개 이상의 독립변수의 수준 변화가 종속변수에 미치는 효
과를 조사하는 데 사용
- 이원분산분석: 2개의 독립변수의 수준 변화가 종속변수에 미치는 효과 분석
♤ 예시
- 일원분산분석: 소비자의 제품사용량에 따라 시리얼 브랜드 선호도 차이
- 이원분산분석: 제품사용량과 나이에 따라 시리얼 브랜드 선호도 차이

(4) 분산분석의 절차

2) 분산분석의 적용 과정
(1) 사례 설정
| ♤ O社는 분말 형태의 세탁 세제를 판매하고 있는데, 최근 두 달간 매출감소를 만회하기 위해 다음 달부터 판촉 프로그램을 계획하고 있음 ♤ 이를 위해 현재 20% 가격 인하와 판촉물을 제공하는 방법 중 보다 효과적인 판촉 수단을 선택하기 위해 서울 시내 15개 슈퍼마켓을 표본으로 선정하여 판촉 유형이 매출액에 미치는 효과를 조사하기로 결정함 |
(2) 분석 환경 설정
♤ 총 15개 점포에 대해 5개는 아무런 판촉을 실시하지 않고, 다른 5개에 대해서는 20% 가격
인하, 또 다른 5개에 대해서는 제품 가격의 약 20%에 상당하는 판촉물(플라스틱 용기 또는
자사의 샴푸 중 하나 선택)을 제공함
♤ 이를 통해 다음과 같이 판촉 유형에 따른 점포 별 매출증가율 자료가 조사됨
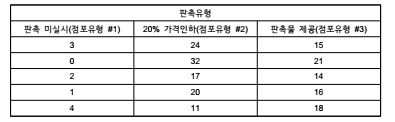
(3) 가설 설정
♤ 분산분석에서 귀무가설은 ‘각 집단의 종속변수 평균값이 동일하다’는 것
♤ 즉, 독립변수(본 사례에서는 판촉형태)가 종속변수(매출)의 변화에 영향을 주지 못한다는 것
이 귀무가설이라 할 수 있음
♤ μ1, μ2, 그리고 μ3를 각각 판촉형태 별 집단의 매출 평균값이라 하고, 그 평균값의 차이가
있는 지의 검증을 위해 다음과 같이 가설 설정을 함

♤ 이는 본 사례에 적용 시 다음과 같이 가설로 설정될 수 있음

(4) 분산분석 시, 필요로 하는 집단 특성에 대한 가정의 검토
♤ 분산분석 적용 시, 다음의 전제조건을 충족시키고 있는지에 대한 검토가 필요함
| ♤ 각 집단은 서로 독립적이어야 함. 즉, 한 집단에 대해 시간 간격을 두고 세 번 종속변수의 값을 측정한 후 이들 간의 차이를 조사하는 경우는 각 집단이 동일하므로 분산분석의 적용이 어려움 ♤ 각 집단은 정규분포를 이루어야 함. 이를 충족시키기 위해 집단별로 표본의 수가 30명 이상 되는 것이 바람직하며, 어느 한 집단의 표본 수가 적은 경우 해당 집단을 제거하든지 혹은 가장 유사한 집단과 합쳐 분석을 해야 함.(예. 학력별 백화점 이용실태 조사 시, 중졸 이하나 대학원 이상의 학력을 가진 응답자가 적은 경우 이들을 분석에서 제외하거나 고절 이하나 대졸 이상 집단에 포함시켜 분석을 하는 것이 권장됨 ♤ 집단 별 분산(variance)의 정도가 비슷해야 함. 분산의 정도가 비슷할 때, 평균의 비교가 의미 있으나 분산의 차이가 클 때, 평균 비교가 의미가 없을 수 있음(A, B는 평균의 비교가 의미가 있으나, A, C는 의미를 가지지 못할 수 있음) 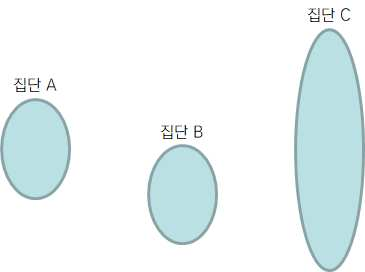 |
(5) 검증통계량의 계산
♤ 분산분석에서 가설검증을 위해 사용되는 통계량은 F통계량임
- 종속변수의 각 관찰값(본 사례에서는 집단 별 각 점포의 매출액)을 ‘전체 평균과 집단 평
균 간의 차이’와 ‘집단평균과 개별 관찰치와의 차이’로 구분하고, 이들 차이의 크기를
토대로 집단 간 차이가 유의한지를 검토하게 됨
| 총편차(전체평균 – 개별관찰값) = 집단 간 편차(전체평균 – 집단평균) + 집단 내 편차(집단평균 – 개별관찰값) |
이를 세가지 변량의 형태로 재설계하면
| 총변량(SST, Sum of Squaress Total) = 집단 간 변량(SSB, Sum of Squaress Between groups) + 집단 내 변량(SSW, Sum of Squaress Within groups) |
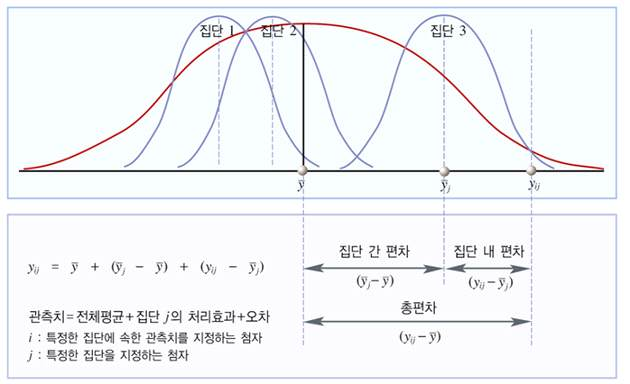
♤ 총변량(SST, Sum of Squares Total): 각 관찰값들이 전체 표본의 평균을 중심으로 얼마만
큼의 변량을 보이는가를 측정하는 것

♤ 집단간 변량(SSB, Sum of Squares Between groups): 독립변수(판촉유형)에 의해 나누어
진 각 집단(판촉을 실시하지 않은 집단, 가격인하 집단, 판촉물 제공 집닫)의 평균이 전체 표
본의 평균을 중심으로 어느 정도의 변량을 보이는 지를 측정하게 됨

♤ 집단내 변량(SSW, Sum of Squares Within groups): 각 표본집단 내 개별 관찰치들이 각
표본집단의 평균을 중심으로 어느 정도의 변량을 보이는지를 측정함

♤ 집단 간 변령과 집단 내 변량이 산출되면 이를 이용하여 집단 간 차이를 검증할 수 있음
- 분산분석에서 집단 간 차이가 유의하기 위해서는 ① 집단 내 변량은 가능한 적어야 하고,
② 집단 간 변량은 가능한 커야 함
- 즉 유의성 검증을 위해서는 집단 간 변량과 집단 내 변량의 상대적 비율을 활용하게 됨
- 이를 F통계량이라 함

♤ F통계량의 계산을 위한 과정은 분산분석표(ANOVA Table)로 요약될 수 있음
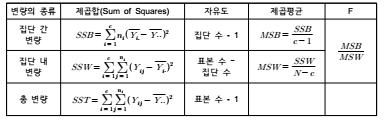
♤ 판촉유형 별 세탁세제 매출효과에 대한 사례에 대한 분산분석표는 다음과 같이 작성됨

(6) 유의성 검증과 결과 해석
♤ 조사자는 집단 간 차이에 대한 가설 검증을 위해 분산분석표를 이용하여 계산된 F통계량과
비교하기 위한 기준값인 임계치를 설정해야 함
♤ F통계량은 자유도 ‘집단 수 – 1’과 ‘표본 수 – 집단 수’의 F분포를 따르게 됨
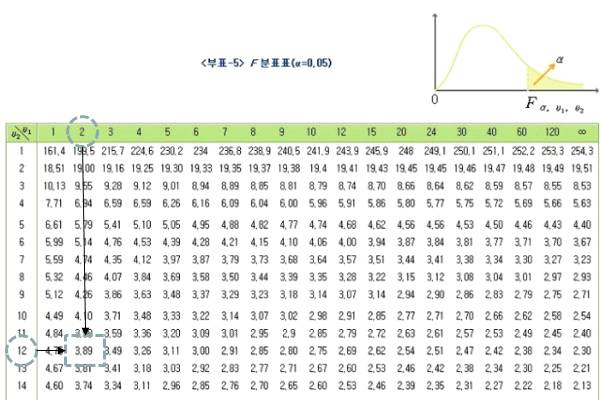
♤ F-value는 20.46으로 임계치 3.89보다 훨씬 큰 것으로 나타남에 따라 집단 간 평균의 차이
가 없을 것이라는 귀무가설을 기각하게 됨
♤ 즉 2가지 판촉 방법 모두가 의미가 있게 매출을 증가시키는 것으로 결론을 내릴 수 있음
3) 실험설계 유형에 따른 분산분석의 종류
(1) 사례 설정
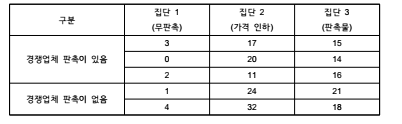
| ♤ 앞에서 설정된 사례 중 우리 회사뿐만 아니라 경쟁기업에서도 동시에 판촉을 진행하고 있는 경우가 있어 이에 대한 고려가 요구됨 ♤ 즉 경쟁업체의 판촉이 있는 경우와 없는 경우가 우리 회사 매출에 영향을 미치는 효과를 반영할 수 있어야 함 |
(2) 분석 환경 설정
♤ 총 15개 점포에 대해 5개는 아무런 판촉을 실시하지 않고, 다른 5개에 대해서는 20% 가격
인하, 또 다른 5개에 대해서는 제품 가격의 약 20%에 상당하는 판촉물(플라스틱 용기 또는
자사의 샴푸 중 하나 선택)을 제공함
♤ 이를 통해 다음과 같이 판촉 유형에 따른 점포 별 매출증가율 자료를 작성해야 함
(3) 분산분석 방법
♤ 일원분산분석(One-way ANOVA) 방법과 동일하나, 개발관찰치의 총변량을 ‘집단 간 차이,
통제변수 간 차이, 그리고 집단 내 차이’로 분리하여 도출하는 점에서 차이가 있음
♤ 즉 ‘통제변수간 차이’를 고려함으로써 통제변수의 효과를 반영한다는 점
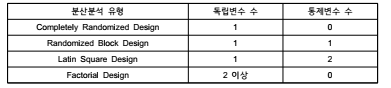
독립변수와 통제변수의 수에 따른 분산분석 유형
4) 다원분산분석을 이용한 가설검증
(1) 사례 설정
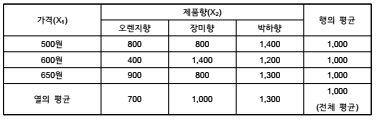
| ♤ L社의 치약제품 마케팅 책임자는 제품향(오렌지향, 장미향, 박하향)과 가격 수준(500원, 600원, 650원)이 매출에 미치는 효과를 조사하려고 함 ♤ 이를 위해 3가지 제품향과 3가지 가격의 조합에 의해 9개의 시제품을 개발한 후 유사한 소매점포를 9개 선정하여 각 점포별로 하나의 시제품만을 취급하도록 함 |
(2) 분석 환경 설정
♤ 각 점포별 시제품의 판매량은 다음과 같이 조사됨
(3) 가설 설정
♤ 독립변수에 대한 각각의 효과와 독립변수 간 상호작용효과에 대한 가설이 설정되어 검증이
수행됨
♤ 독립변수 각각의 효과에 대한 가설

♤ 독립변수 간 상호작용효과에 대한 가설*

- 본 예시에서는 상호작용효과가 없을 것으로 가정하고, 이에 대한 검증은 생략함
♤ [참조] 상호작용의 의미
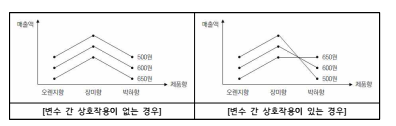
(4) 검증통계량의 계산
♤ 이원분산분석도 변량을 활용한 F통계량이 상요됨
♤ 이를 위해 독립변수 X1과 X2가 각각 C1, C2개의 범주로 나누어진다고 가정하고, 이를 바탕
으로 총변량을 구하면 다음과 같음

♤ 이를 토대로 산출된 분산분석표는 다음과 같음
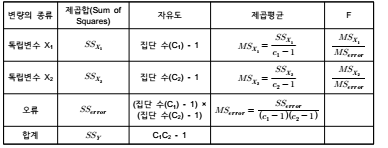
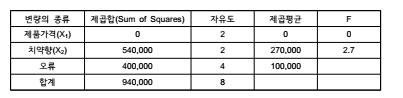
(5) 유의성 검증 및 결과해석
♤ 유의수준 0.05, 분자 자유도 2, 분모 자유도 4 F분포의 임계치는 6.94
♤ F통계량은 0, 2.7이므로 임계치보다 작음. 따라서 귀무가설이 유지됨(채택됨)
♤ 따라서 제품 가격의 변화와 치약향의 유형이 시제품의 판매량에 영향을 미치지 않는다고 결
론 내릴 수 있음
'시장조사론' 카테고리의 다른 글
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 47. 상관계수의 의미 (0) | 2024.06.30 |
|---|---|
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 46. 상관관계 분석 개념 (2) | 2024.06.28 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 44. 두 집단 간 비율차이 가설검증 (1) | 2024.06.25 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 43. 두 집단 간 평균차이 가설검증 (2) | 2024.06.19 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 42. 통계기법의 구분 (1) | 2024.06.18 |



