43. 두 집단 간 평균차이 가설검증
1) 집단 간 차이 분석을 위한 필요성
(1) 마케터는 세분시장 도출과 목표시장 선정을 위해 남녀별, 연령별, 또는 주거지역
별로 선호하는 브랜드 또는 선택하는 브랜드에 대한 차이가 있는 지 등을 알고 싶어함
(2) 또한 여당이나 야당은 선거 전 지역별로 유권자들의 정당 후보자에 대한 지지도
차이를 알고 싶어함
(3) 즉 집단 별로 어떤 특성에서 차이가 있는 지를 파악하고자 할 때 이용되는 통계
기법이 ‘집단 간 차이 검증을 위한 통계분석’이며 종속변수의 척도 유형에 따라
이용되는 분석기법이 달라지게 됨
2) 두 집단 간 평균차이에 대한 검증 필요성
(1) 두 집단 간 평균차이에 대한 검증 목표와 범위
■ 서로 독립적인 두 집단의 평균 간에 차이가 있는 지의 여부. 즉 서로 배타적이고 독립적인
두 집단 간의 평균이 차이가 있는 지의 여부 검증(예. 남성과 여성 간 음료 구매량에서의 차
이가 있는 지의 여부)
■ 동일집단에 대해 마케팅 자극을 노출하기 전과 노출한 후의 효과 검증. 즉 한 모집단 내 표
본의 값이 짝(pair)을 이루고 있고, 이 값들 간의 차이가 있는 지의 여부 검증(예. 새로운 광
고의 방영 전후에 따라 제품 선호도 차이가 있는 지의 여부)
3) 두 집단이 독립적*인 경우
(1) 사례 설정
| ■ H社는 ⓐ 타이어 전문대리점과 ⓑ 카센터의 2가지 유통경로를 이용하여 타이어를 유통 및 판매하고 있는 중임. 예산 상의 문제로 인해 두 유통경로 중 하나에 대해서만 판촉 계획을 고려하고 있음 ■ 이를 위해 우선적 지원을 위한 유통경로를 선택하기 위해 전문대리점 및 카센터를 각각 100개 추출하여 현재 본사 지원에 대한 만족도를 7점 척도를 통해 측정하고, 그 결과 만족도가 상대적으로 낮은 유통경로에 대한 지원을 추진할 계획임 |
- 독립적이라 함은 한 집단에 대한 측정이 다른 집단의 측정에 영향을 미치지 않는다는 것
(2) 가설의 설정
■ 전문대리점 및 카센터의 만족도 점수에 대한 평균을 각각 μ1, μ2라고 하면 양측 검증에 해당
하는 가설이 설정됨
■ H0: μ1 = μ2
■ Ha: μ1 ≠ μ2
■ 이는 현재 전문대리점과 카센터 중, 어느 곳이 높아진 지에 대해서 알 수가 없기 때문임. 다
만 과거 경험이나 조사를 통해 어느 한 곳이 높은지를 추정할 수 있을 때는 단측 검증을 사
용할 수도 있음
■ H0: μ1 < μ2
■ Ha: μ1 ≥ μ2
(3) 검증통계량 및 가설채택기준의 결정
■ 두 집단 간 평균 차이에 대한 가설 검증에서는 t통계량이 사용됨

■ 본 조사에서 가설채택의 기준으로 유의수준 α=5%를 이용하며, 본 검증이 양측검증임에 따
라 다음과 같이 양쪽으로 각각 2.5%씩 할당됨

(4) 가설채택여부의 결정
■ 각 유통경로에 대해 100개씩 표본으로 선출된 점포들에 대해 만족도를 조사한 결과는 다음
과 같음
| 구분 | 집단 1(대리점) | 집단 2(카센터) |
| 만족도 평균 | 4.4 | 4.7 |
| 표본의 수 | 100 | 100 |
| 만족도의 표준편차 | 1.0 | 0.9 |
■ 위의 결과를 토대로 t통계량은 다음과 같이 산출됨
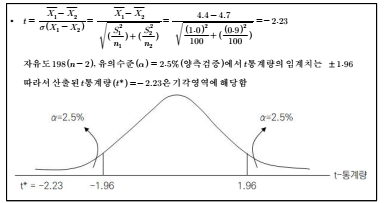
■ 이는 두 집단 간 만족도 점수의 평균에 대한 차이가 없다는 귀무가설이 기각되며, 두 집단
간의 만족도 차이가 있다는 대립가설은 통계적으로 유의함
■ 따라서 마케팅 담당자는 만족도 점수가 낮은 대리점에 대한 더 많은 지원을 해야 하는 것으
로 결론이 남
4) 한 집단에서 짝을 이룬 값들의 차이를 검증하는 경우
(1) 사례 설정
| ■ L사는 최근 판매가 부진한 탄산음료 A에 대한 개선방안으로 제품의 속성(당분 및 향)을 바꾸어 신세대를 겨냥한 신제품을 출시하려는 계획을 세우고 있음 ■ 제품 출시에 앞서 신세대들의 반응을 보기 위해 100명의 표본을 선정하여 기존 제품과 신제품에 대한 시음 조사를 실시하였음 ■ 두 제품에 대한 구매의사를 5점 척도를 이용하여 비교, 평가하도록 하여 신제품이 기존제품보다 높은 평가를 받은 경우에 한하여 제품을 출시하기로 함 |
(2) 가설의 설정
■ 표본의 값이 짝을 이루고 있고, 이들간 차이가 있는지의 여부를 검증하는 경우 각 표본값의
평균을 직접 비교하지 않고, 두 표본값의 차이가 0인지의 여부*를 검증하는 간접적 방법을
이용하게 됨
- 차이가 0이라 함을 두 값이 동일함을 의미함
■ 즉 두 표본값 차이의 평균이 0인지의 여부를 검증하는 것으로 단일집단 평균에 대한 검증과
유사하게 됨
■ 따라서 이 경우 다음과 같이 가설이 설정되며, 단측 검증을 통해 검증이 실시됨
■ H0: d = 0
■ Ha: d > 0
■ d: 쌍을 이룬 표본값들의 차이를 말하며, 여기서는 (‘신제품에 대한 구매의사점수’ – ‘기존
제품에 대한 구매의사점수’)를 의미함
(3) 검증통계량 및 가설채택기준의 결정
■ 이 경우 이용하는 검증통계량은 t통계량이며 이는 n-1의 자유도를 갖는 t분포를 따르게 됨

(4) 가설채택여부의 결정
■ 100명의 표본을 측정한 결과, 결과차이의 평균은 0.4, 차이의 표준편차는 0.25로 나타남
■ 이에 따라 t통계량은 다음과 같이 산출됨
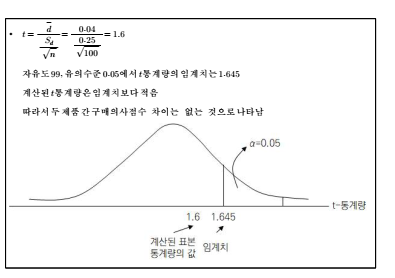
■ 이는 기존 제품과 신규 제품 간 구매의사에 대한 점수의 평균에 대한 차이가 없다는 귀무가
설이 채택됨을 의미함
■ 따라서 마케팅 담당자는 신세대의 기호를 보다 잘 반영할 수 있도록 신제품의 개선을 추진
하여야 함
5) 두 집단 간 평균차이에 대한 가설 검증을 위한 SPSS 프로그램 사용
(1) 두 집단이 독립된 경우의 T-test
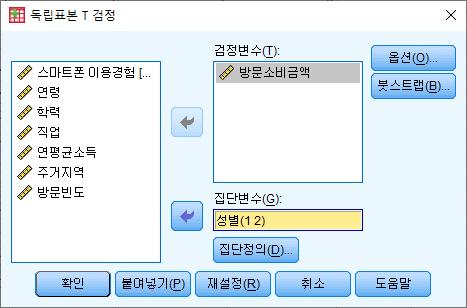
■ [분석] - [평균비교] - [독립표본T-검정]을 통해 수행할 수 있음
- 검정변수: 종속변수에 해당하는 변수를 지정하면 됨. 본 예시에서는 방문소비금액을 검증
하고자 함
- 집단변수: 차이를 보기 위한 2개 집단을 정의함. 성별 1(남성), 2(여성)을 통해 지정
■ 결과 해석
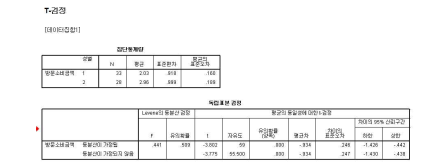
- T-test를 통해 나타난 결과는 등분산*이 가정된 경우, 등분산이 가정되지 않은 경우의 2
개로 볼 수 있음. 이는 F값의 유의확률을 통해 확인할 수 있음. 현 사례에서는 F값의
유의확률이 0.509로 유의수준보다 높아 귀무가설, 즉 등분산이 채택됨
- 2개의 모집단에서 추출된 표본의 분산(variance)이 동일하다는 것을 의미함
- 따라서 등분산이 가정된 t-값을 토대로 검증한 결과 –3.802이고, 유의확률은 0.000으로 2
개 집단 간 차이가 ‘있음’을 알 수 있음
(2) 짝을 이룬 값들의 차이 검증(동일한 표본에 대해 2회 반복측정한 경우의 차이 검
증)을 위한 T-test
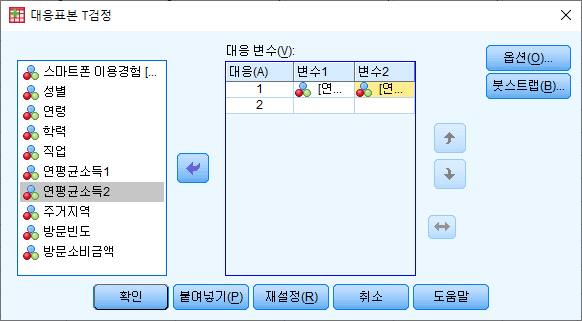
■ [분석] - [평균비교] - [대응표본T-검정]을 통해 수행할 수 있음
- 대응변수: 첫 번째 측정한 변수와 두 번째 측정한 변수를 각각 지정하면 됨. 본 예시에서
는 연평균소득의 변화를 보기 위해 초기 측정한 ‘연평균소득1’과 1년 후에 측정한 ‘연평
균소득2’를 대응변수로 설정함
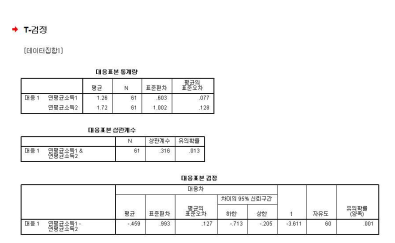
■ 결과 해석
- 연평균소득1과 연평균소득2 간의 차이가 있음을 의미하는 t-값은 –3.611로 유의확률이
0.001로 나타남에 따라 유의수준 0.05보다 작음
- 따라서 연평균소득1과 연평균소득2 간의 차이는 ‘있음’으로 판단할 수 있음
'시장조사론' 카테고리의 다른 글
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 45. 분산분석 (1) | 2024.06.27 |
|---|---|
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 44. 두 집단 간 비율차이 가설검증 (1) | 2024.06.25 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 42. 통계기법의 구분 (1) | 2024.06.18 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 41. 단일모집단 평균과 비율에 대한 가설검증 (2) | 2024.06.17 |
| 경영학, 경제학, 경영지도사 대비 시장조사론 핵심 요점 정리 40. 가설검증의 의미 및 절차 (2) | 2024.06.16 |



