컴퓨터공학, 컴활, 컴공 등 데이터베이스 과목 핵심 요점 정리 3. Hashing(3)

3장. Hashing(3)

 

(1) 충돌 해결 기법의 개요

① 충돌(collision)이란?

󢐠충돌(collision) : 어떠한 레코드를 파일에 저장하기 위해 주소를 계산하여 넣으려고 하는데, 이미 그 자리에 다른 레코드가 저장되어 있는 경우

→ 그 레코드를 저장하기 위한 다른 곳을 결정

→ 레코드를 검색할 때 자신의 홈 어드레스에 있지 않으므로, 옮겨 간 위치를 찾을 수 있도록 해야 한다.

 

② 충돌 해결 방법의 종류

󢐠개방주소법(open addressing)

▹ 오버플로된 레코드가 저장될 위치를 결정하는 규칙을 정의하여 이 규칙에 따라 레코드를 저장하고 검색하는 방법

󢐠체인법(chaining)

▹ 오버플로 된 레코드가 저장된 위치를 포인터로 연결하는 방법

 

(2) 개방주소법(Open addressing)

①-1 개방주소법의 개요

󢐠개방주소법(Open addressing)

△ 키로부터 일련의 버켓 주소를 생성할 수 있는 함수를 정의한다.

Ai = f(i, 키), i=0, 1, 2, …

▹ i : 조사 순번

▹ f : i와 키의 함수

△ 레코드의 삽입 : A0, A1, A2, … 의 순으로 버켓을 조사하다가 첫 번째로 발견되는 빈 공간에 레코드를 저장한다.

△ 레코드의 검색 : 저장할 때와 동일한 순서대로(즉, A0, A1, A2, … 의 순) 검색하고자 하는 레코드가 발견될 때까지 버켓을 액세스한다.

- 레코드가 발견되기 전에 빈 공간을 만나면 검색은 실패

②-2 개방주소법의 개요

(예) 레코드 R을 삽입하는 삽입 과정

△ R에 대한 주소 시퀀스가 A0=13, A1=15, A2=20 … 라 할 때 13번지와 15번지에 다른 레코드가 저장되어 있으므로 R은 20번지에 저장한다.

☞ R이 파일에 기록되기 위해서는 3회의 버켓 판독(13, 15, 20번지)과 1회의 기록(20번지)이 필요하다.

③-1 선형조사(Linear Probing)

󢐠주소 시퀀스의 계산 : 조사하는 주소 시퀀스가 선형적으로 변화한다.

③-2 선형조사(Linear Probing)

■ 문제점 : 집중현상

△ 기본집중(primary clustering) : 주소의 조사 간격이 레코드의 키나 조사 순서에 무관하게 일정하다. 따라서 서로 다른 두 키의 조사 시퀀스 중 어느 한 곳에서 같은 주소가 발생하면 그 이후로는 계속 같은 주소를 조사하게 된다.

 

 

③-3 선형조사(Linear Probing)

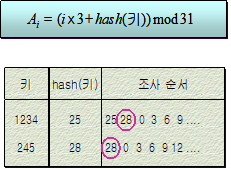
(예) Ai = (i×3 + hash(키)) mod 31

△ 키가 1234인 레코드의 조사순서와 키가 245인 레코드의 조사순서 중 같은 값(28)이 나온 후 계속 같은 주소를 조사한다.

③-4 선형조사(Linear Probing)

△ 집중현상의 문제점 : 연속적인 오버플로가 발생함으로써 파일의 효율이 크게 떨어진다.

(예) 10개의 버켓에 레코드가 그림과 같이 채워져 있을 때 각각의 버켓에 레코드가 저장될 확률이 균일하지 않다. (조사간격(step)이 1이라고 할 때)

- 4번 버켓이 홈 어드레스인 레코드와 5번 버켓이 홈 어드레스인 레코드의 경우 5번지부터 조사 순서가 동일하므로 만일 4번지가 홈 어드레스인 레코드를 삽입하려고 하면 연속적으로 충돌을 일으키게 된다.

※ 기타

④-1 비선형조사

■ 주소 시퀀스의 계산 : 조사 시퀀스를 선형함수와 같이 고정된 간격으로 변화시키지 않고 비선형 함수에 따라 변화시켜서 조사 순번에 따라 간격을 다르게 한다.

Ai = (g(i) + hash(키)) mod N, i=0, 1, 2, …

선형조사 : g(i)가 i의 선형 함수

비선형 조사 : g(i)가 i의 비 선형 함수

→ 조사 시퀀스 중 같은 주소가 발생되더라도 순번 i가 다르면 이후에는 다른 주소가 발생된다.

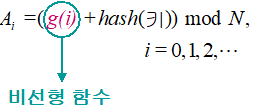
④-2 비선형조사

(예) Ai = (i×3 + i2×5 + hash(키)) mod 31

△ 키가 1234인 레코드와 키가 100인 레코드의 조사 시퀀스 중에 2번지가 모두 포함되어 있지만 순번이 다르기 때문에 그 이후에는 다른 순서로 버켓을 조사하게 된다.

△ 제2차 집중

- 홈 어드레스가 같은 경우에는 역시 동일한 조사 시퀀스를 가지게 된다.

⑤ 이중해싱

■ 주소 시퀀스의 계산 : 2개의 해싱함수를 사용

A0 = hash(키)

Ai = (Ai-1 + hash'(키)) mod N, i=1, 2, …

△ hash(키) : 홈 어드레스를 결정

△ hash'(키) : 선형조사와 비교해 보면 조사 간격(step)에 해당되는데, 이를 해싱함수로 계산함으로써 레코드마다 조사 간격이 다르게 한다.

 

 

(예) hash(키) = 키 mod 31

hash'(키) = 1 + ⌊키/31⌋ mod 29

→ 1234, 366, 831이 모두 홈 어드레스가 동일하지만 조사 시퀀스는 모두 다르다.

■ 이중해싱의 특성

△ 집중현상을 완화함으로써 연속적인 충돌을 방지하여 파일의 효율을 높인다.

△ 조사 간격이 주소공간의 크기 N의 인수라면 주소공간을 모두 조사하지 못하게 된다. 따라서 N은 소수이거나 인수가 작은 값을 포함하지 않는 수이어야 한다.

△ 조사 간격이 큰 값일 경우 조사할 버켓이 다른 실린더에 존재할 수 있으며, 이 때 헤드의 탐구시간이 많이 소비된다.

 

⑥ 개방주소법에서의 연산

※ 조사간격이 1인 선형조사를 활용하는 예

■ 레코드의 삽입

△ R1 삽입 : 홈 어드레스인 5번지가 비어 있으므로 5번지에 삽입

△ R2 삽입 : 홈 어드레스인 7번지가 비어 있으므로 7번지에 삽입

△ R3 삽입 : 홈 어드레스인 5번지에 이미 다른 레코드가 있으므로 step(이 예에서는 1) 만큼 이동하여 6번지를 조사한다. 6번지가 비어 있으므로 R3를 6번지에 저장한다.

△ R4 삽입 : 홈 어드레스인 6번지에 이미 다른 레코드가 있으므로 step 만큼 이동하면서 빈 공간을 찾는다. 결국 8번지가 비어 있음을 발견하고 그 곳에 R4를 저장한다.

■ 레코드의 검색

△ R1의 검색 : 홈 어드레스인 5번지에서 레코드 검색 성공

△ R4의 검색 : 홈 어드레스로부터 버켓을 조사하여 8번 버켓에서 검색 성공

△ R5(홈 어드레스가 7번지)의 검색 : 7번지로부터 시작하여 차례로 버켓을 조사하다 보면 빈 버켓을 만나게 되므로 검색 실패

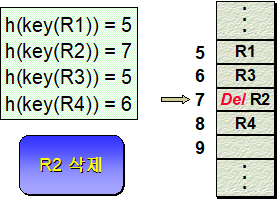
■ 레코드의 삭제 - R2의 삭제

△ R2를 완전히 삭제할 경우 R4와 같이 R2 때문에 충돌이 발생하여 다른 위치에 저장된 레코드들은 검색할 수 없다.

△ 완전히 삭제를 하지 않고, ‘삭제’ 표시를 하면 레코드를 검색할 때 ‘삭제’ 표시된 공간을 빈 공간으로 보지 않음으로써 R4와 같이 이동된 레코드를 검색할 수 있다.

☞ 새로운 레코드를 삽입할 때 ‘삭제’ 표시된 공간은 빈 공간으로 본다.

☞ 레코드를 검색할 때 ‘삭제’ 표시된 공간은 레코드가 채워져 있는 공간으로 본다.

☞ 레코드가 삭제되었지만 완전히 빈 공간이 되지 않기 때문에 레코드를 검색할 때 효율이 저하된다.

→ 삭제 표시된 레코드가 많을 경우 파일을 재구성하여 삭제 표시된 영역을 제거함으로써 레코드 검색 효율을 높인다.

(3) 체인법(Chaining)

① 체인법 개요

■ 체인법(chaining)

△ 오버플로 된 레코드들을 적절한 빈 공간에 저장한 후 이를 검색할 수 있도록 포인터로 연결한다.

△ 오버플로 된 레코드를 저장하는 공간

a. 기본구역의 미사용 공간을 사용하는 방법

b. 별도의 오버플로 구역을 설정하는 방법

 

 

② 연합 리스트

1) 연합 리스트

■ 오버플로가 발생하면 그 레코드를 기본구역 내의 비어 있는 공간에 레코드를 저장한 후 홈 어드레스로부터 시작되는 오버플로 체인에 연결한다.

☞ 오버플로 된 레코드를 저장한 공간은 차후에 입력되는 다른 레코드의 홈 어드레스가 될 수 있으며, 이 경우 홈 어드레스가 서로 다른 레코드가 한 체인에 연결될 수 있다. 이와 같이 되면 오버플로 체인의 길이가 길어져서 레코드를 검색할 때 액세스 횟수가 많아져 효율이 저하될 수 있다.

 

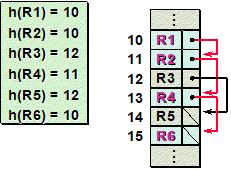
(예) R1～R6를 차례로 삽입

△ R1, R2, R6의 홈 어드레스 = 10

△ R3, R5의 홈 어드레스 = 12

△ R4의 홈 어드레스 = 11

 

(예) 레코드의 검색 연산

△ R1 검색 : 홈 어드레스에서 검색됨

△ R4 검색 : 홈 어드레스인 11번지에 같은 키를 갖는 레코드가 없고 다른 레코드가 있음

→ 체인을 따라 검색하여 13번지에서 검색함

※ 문제점 : R1, R2, R6의 오버플로 체인에 R4가 함께 연결되어, 불필요하게 체인의 길이가 길어져 검색 효율이 저하된다.

■ 2단계 적재 방법으로 파일 생성

◦ 1단계 : 홈 어드레스에 저장될 수 있는 레코드들만 적재하고, 나머지 레코드들은 임시 파일에 저장한다.

◦ 2단계 : 임시 파일에 저장되어 있는 레코드들을 적재한다.

 

■ 2단계 적재를 한 후 레코드의 추가 삽입이 이루어지면 다시 연합 리스트가 만들어질 수 있다.

→새 레코드를 삽입할 때 필요하면 레코드를 이동하여 불필요하게 체인이 길어지지 않도록 한다.

(예) 홈 어드레스가 13번지인 R7의 삽입

▪ 13번지에 저장되어 있던 레코드 R2의 홈 어드레스가 13번지인가 검사

▪ 그렇지 않다면 R2를 다른 빈 곳으로 이동시킨 후 포인터를 조정

▪ R7을 자기 자신의 홈 어드레스인 13번지에 저장

③ 오버플로 구역의 활용

■ 전체 공간을 기본구역과 오버플로 구역으로 분할한다.

■ 주소비율 : 전체 공간 중 기본구역이 차지하는 비율

△ 주소비율이 낮으면 홈 버켓의 수가 줄어들어 충돌이 발행할 확률이 커지고, 반대로 너무 높으면 오버플로된 레코드를 수용하는데 어려움이 있다.

△ 주소비율이 0.86인 경우 최적의 효율을 낸다는 실험 결과가 있다.

(예) R1～R6의 삽입

(예) 레코드의 삭제

△ 오버플로 구역에 있는 레코드(예 : R2)의 삭제 : 레코드를 삭제하고 포인터를 변경하면 된다.

△ 기본구역에 있는 레코드(예 : R3)의 삭제 : 레코드를 삭제한 후 오버플로 체인에 연결된 레코드 하나를 기본구역으로 이동시킨다.

△ 홈 어드레스가 다른 레코드들이 한 체인에 연결되지 않는다.

△ 오버플로 구역과 기본구역이 분리되어 있어서 오버플로 구역에 있는 레코드를 액세스할 때 헤드의 이동 거리가 길다.