컴퓨터공학, 컴활, 컴공 등 데이터베이스 과목 핵심 요점 정리 2. Hashing(2)

2. 직접파일의 설계 요소

주소를 지정하여 원하는 레코드를 직접접근 할 수 있도록 하려면 레코드의 주소를 결정하는 것뿐만 아니라 앞 절에서 언급한 충돌 문제 등을 고려하여 효율적으로 데이터를 액세스할 수 있도록 하기 위한 몇 가지 설계 요소가 필요합니다. 여기에서는 직접파일을 구현하기 위해서 설계해야 할 내용은 어떤 것들이 있는지 생각해 봅시다

 

⑴ 충돌과 직접파일의 성능

충돌이 발생하면 레코드를 홈 어드레스에 넣지 못하므로 그 주소의 기억공간에서 오버플로가 발생하게 된다. 이 경우 저장하지 못한 레코드를 다른 대체 저장 위치에 저장해야 한다. 이 과정에서 파일 액세스 횟수가 증가한다. 그러므로 오버플로를 최대한 줄이는 것이 필요하다.

 

① 주소공간의 균일한 활용

→ 주소를 계산하는 함수의 결과가 일부 주소에 편중된다면 그 주소에서 많은 충돌이 발생하게 된다.

→ 이상적인 주소 발생 분포는 모든 N개의 주소가 고르게 사용되는 분포이다. 만일 실제로 발생되는 레코드들에 대해 각각의 주소 발생 확률이 모두 1/N 이라면 충돌이 발생하지 않는다. 그러나 실제로는 이러한 분포가 나오기 어려우며, 가능하면 이에 근사한 분포를 갖도록 함수를 설계해야 한다.

② 적절한 적재밀도의 유지

실제로 저장하려는 레코드 수보다 더 많은 레코드를 저장할 수 있도록 저장 공간에 여유를 두면 충돌 발생 가능성을 줄일 수 있다. 파일 내에 얼마나 레코드가 채워져 있는가를 나타내는 인수를 적재밀도(packing density)라고 한다.

→ 적재밀도가 너무 높으면 충돌 발생 빈도가 높아져서 레코드 액세스 효율이 나빠진다.

→ 적재밀도가 너무 낮으면 빈 공간이 많이 남아 저장공간을 낭비한다.

→ 적절한 적재밀도 : 70~80%

 

③ 한 주소에 여러 개의 레코드 저장

직접파일에서 하나의 주소로 지정되는 공간에 레코드를 여러 개 넣을 수 있도록 하는 것을 생각해 볼 수 있다. 이러한 아이디어는 자기디스크장치에서 매우 자연스럽다. 자기디스크는 블록단위의 액세스를 하기 때문에 주소를 블록과 연관지을 수 있기 때문이다.

이러한 아이디어에 따라 직접파일에서는 버켓을 다음과 같이 정의한다.

 

⑵ 적재밀도, 버켓의 크기, 버켓 수와 직접파일의 성능과의 관계

⊙ 오버플로가 발생할 가능성

① 고려할 인수

② 한 버켓에 1개의 레코드가 사상될 확률 P(I)

③ 오버플로를 일으키는 레코드의 비율 R(%)

④ 버켓 수 N이 200인 경우와 1600인 경우 버켓 크기 및 적재밀도에 따른 오버플로 발생 가능성의 관계의 예

▪ 적재밀도가 커질수록 오버플로가 발생할 가능성은 증가한다.

▪ 버켓의 크기가 커질수록 오버플로가 발생할 가능성은 감소한다.

▪ 버켓 수 N이 200인가, 1600인가에 따른 차이는 크지 않다.

 

※ ※ 한 버켓에 5개의 레코드를 저장할 수 있도록 한 경우 버켓의 수 N이 200, 400, 1600일 때 오버플로가 발생하는 비율은 거의 유사하다.

⇒ 직접파일의 성능은 파일의 크기보다는 적재밀도 및 버켓의 크기에 의해 좌우된다.

 

⑶ 직접파일 설계 요소 구현 방법

① 주소 계산 함수의 설계

적재밀도와 버켓의 크기, 저장할 레코드의 수를 고려하여 필요한 주소공간의 크기를 결정한 후 이 범위의 주소를 계산해 낼 수 있는 함수를 정의한다.

주소의 범위를 미리 결정한 후 함수를 정의했기 때문에 파일의 크기를 확장하거나 축소하려면 함수를 다시 정의해야 하고, 이에 따라 레코드의 주소가 모두 바뀔 수 있으며, 이는 파일을 다시 작성하게 되는 결과가 된다. 따라서 파일의 크기는 손쉽게 변화시킬 수 없으며, 이러한 의미에서 이와 같은 직접파일을 정적인 직접파일이라고 한다.

② 충돌 해결 알고리즘 설계

충돌은 언제든 발생할 가능성이 있으므로 이에 대비한 충돌 해결 알고리즘이 반드시 정의되어야 한다.

 

 

⇒ 이러한 기본 요소를 바탕으로 레코드의 삽입, 삭제, 검색, 파일생성 및 재구성 등의 연산을 정의함으로써 직접파일을 구현할 수 있다.

 

3. 해시함수

 

직접파일을 설계할 때 가장 먼저 해야 할 일은 주소를 계산하기 위한 함수를 설계하는 것입니다. 이 함수는 충돌을 최소화할 수 있도록 함으로써 우수한 성능을 낼 수 있도록 하는 첫 걸음입니다.여기에서는 주소를 계산하는 함수의 설계 과정을 자세히 살펴봅니다.

⑴ 해시함수

① 해시함수의 정의

일반적으로 키 값의 공간은 주소 공간에 비해 매우 크며, 그 중 어느 값들이 실제

레코드에서 사용될 것인지를 미리 예측하기 어려우므로, 키 값에 따라 계산되는 값이

주소공간에 뒤섞여 있도록 해시함수를 정의한다.

 

.

② 해시함수의 좋고 나쁨

만일 계산된 주소가 특정 주소에 집중된다면 충돌이 많이 발생하여 파일의 성능이 형편없게 된다. 그러므로 전체 주소공간이 골고루 사용되도록 레코드를 균일하게 주소공간에 사상하는 함수가 바람직하다.

 

해시함수의 Good/Bad

⑵ 해시함수의 유형

대상으로 하는 키의 특성에 따라 적절한 해시함수를 정의하는 것이 좋다.

① 키 값들이 자연적으로 키 공간에 균일하게 흩어져 있는 경우

⇒ 키 공간을 균등하게 분할하는 함수를 정의

 

해시함수의 유형

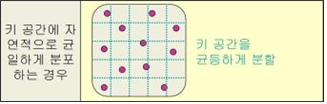
② 키 분포가 균일하지 않은 경우 ⇒ 무작위로 흩어 놓는 함수를 정의

해시함수의 유형2

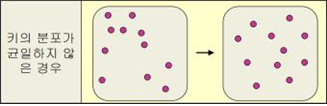
⑶ 해시함수의 주소 변환 과정

① 사용하고자 하는 키의 자료형이 수치형이 아닌 경우는 이를 수치형으로 변환한다.

② 수치형으로 표현된 키를 정해진 자리수의 값으로 변환한다.

③ 변환된 값을 주소 범위의 값으로 조정한다.

⑷ 해시함수의 종류

① 제산잔여 해싱

키 값들이 일련번호와 같은 형태처럼 자연적으로 키 공간에 균일하게 퍼져 있는 경우 적합한 방법이다. 예를 들어 학번을 부여할 때에는 1번부터 차례로 일련번호가 붙이므로, 자연히 키가 균일하게 흩어져 있게 된다.

미리 정한 제수 N으로 나누어 그 나머지를 주소로 사용한다.

주소공간의 크기는 제수와 동일하다.(0~N-1)

제수는 필요한 주소수에 근접한 소수가 적합하다.

 

⑷ 해시함수의 종류

① 제산잔여 해싱

키 값들이 일련번호와 같은 형태처럼 자연적으로 키 공간에 균일하게 퍼져 있는 경우 적합한 방법이다. 예를 들어 학번을 부여할 때에는 1번부터 차례로 일련번호가 붙이므로, 자연히 키가 균일하게 흩어져 있게 된다.

미리 정한 제수 N으로 나누어 그 나머지를 주소로 사용한다.

주소공간의 크기는 제수와 동일하다.(0~N-1)

제수는 필요한 주소수에 근접한 소수가 적합하다.

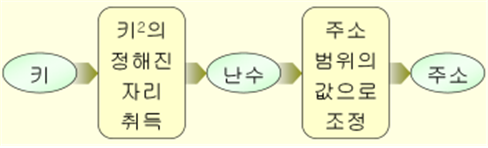
③ 중첩 해싱

키를 정해진 자릿수로 끊어 낸 후, 각 부분의 값을 접어 더하여 값을 만들어 낸다.

◈ 중첩 해싱의 주소 계산 절차

키를 수치형으로 변환한다. ⇒ 키를 정해진 단위로 끊은 다음 방향을 엇갈려 접은 후 중첩하여 합산한다. ⇒ 이 결과를 주소 범위의 값으로 조정하여 주소를 계산한다.